If you spent a large percentage of your life in front of video games, you’re prone to getting seasick or you simply wanted to see if you can set the FOV beyond 180 degrees in your favourite game, you might’ve noticed the distortion present along the edges. Here’s a small selection of examples:

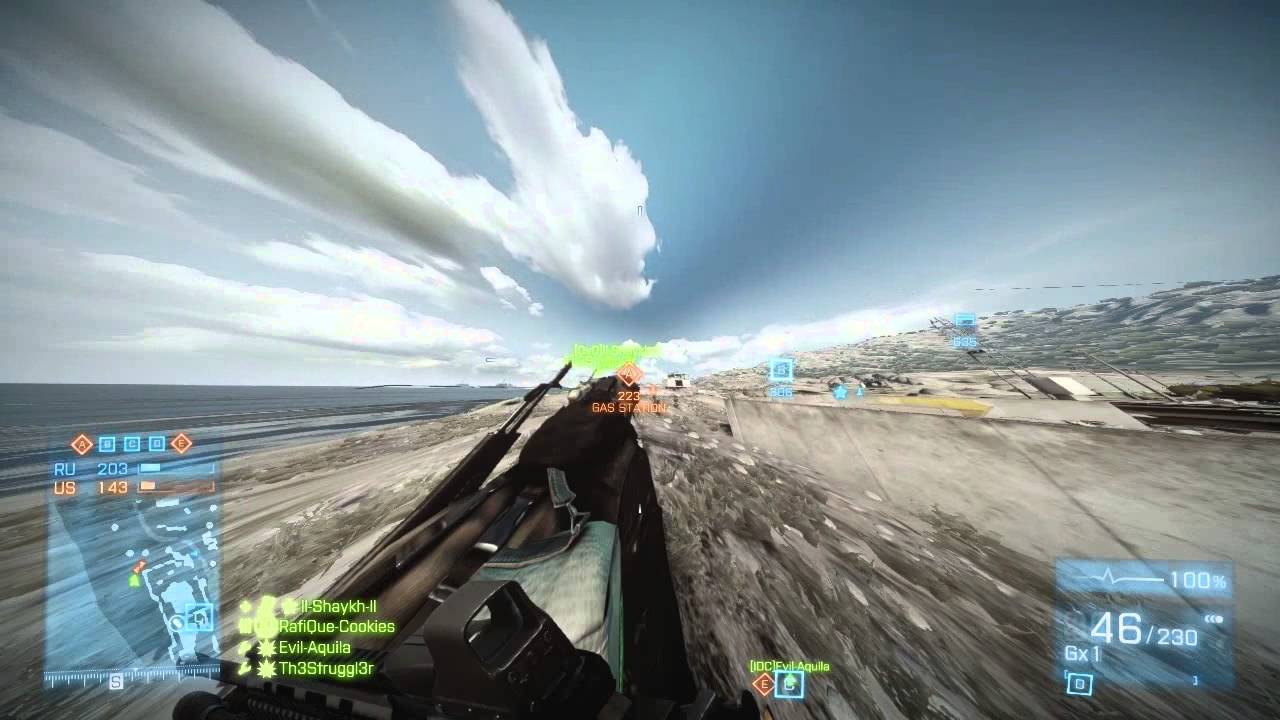
As a side note, most of these games don’t come like this, you have to edit the settings in some way to force it. It was really hard to gather even just these 4 examples, most developers understandably don’t allow you to do this.

There’s also an arbitrary limit on the values you can use, always limited to at most 179 degrees. Is this the fault of the game engine? Or maybe the game developers? Maybe even the GPU manufacturer? Or is this one of the “monkey brain” problems we see so often? The answer to all four is: yes…kind of.

What GPUs can and can’t do

From this point on, we’re talking about games rendered with rasterization. This is the traditional approach, although nowadays we have a fair few examples of ray traced solutions, I’ll talk more about these later.

A rasterized pipeline takes models made out of triangles, transforms them to the correct place on the screen, then fills them in pixel-by-pixel. A big limitation of this approach are the triangles themselves. They have to have straight edges. This means the method we use to create the illusion of depth (the perspective) must preserve the “straightness” of lines (transformations like this are called “linear transformations”).

So, what options do we have?

You can’t make a sphere flat

You might not think what I’m talking about now has anything to do with cartography, but they’re actually part of the same mathematics field. This shouldn’t be too surprising, cartography is about projecting our (roughly) sphere planet onto a (roughly) flat surface and 3D projections are about projecting information coming from all around the camera onto a flat monitor.

Here you might interject with “Uhm actually, I have a curved monitor”. While yes, this could change the result of the projection a bit, there are 3 reasons it doesn’t matter for us right now:

1. A curved plane is still topologically a plane, so projecting a sphere onto it will still cause distortions
2. To properly draw the image on a curved monitor, GPUs would have to be able to draw curved lines, which they can’t as we discussed above.
3. Unless your monitor has a curvature of 50 to 100R (which is literally just the radius in centimeters) you probably don’t sit in the center of the circle it makes, so adjusting for it would be near impossible.

These could kind of mean that flat monitors are objectively better for gaming (for the record I’m running a curved super ultrawide monitor, I’m not biased), but take that however you want to.

Take a look at the demos at the bottom of this article, as you can see, all of those introduce some kind of distortion, and that’s normal! We’re projecting a sphere onto a plane, distortion is inevitable. If you move the camera around, you’ll notice that the only one that preserves straight lines is the planar one, which is why we use it.

So, does that mean we get the distortion, because we’re not using large, spherical monitors?

No, in reality…

The twist

…planar projection is actually distortion free.

You might ask why I can say that so confidently when a couple paragraphs below this very line is a demo clearly showing how much it distorts the edges of the image. The missing link is perspective (literally).

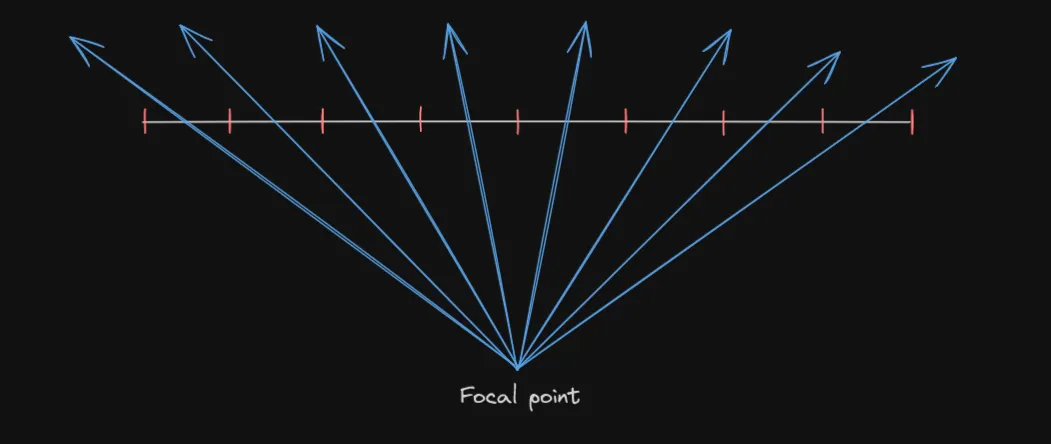
Let’s look at how planar projection works:

Imagine if your monitor consisted of only 8 pixels, each representing a ray going from the focal point toward the center of that pixel:

;

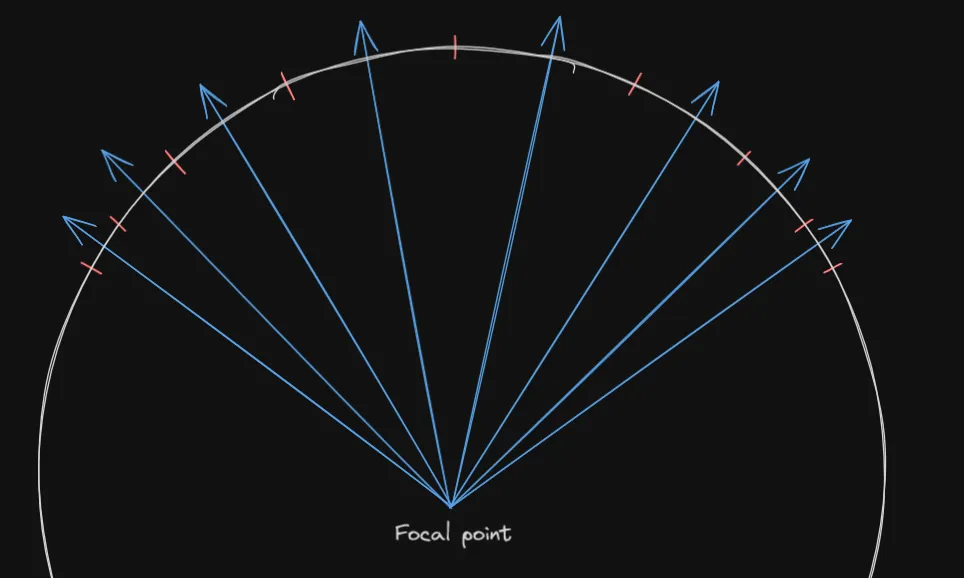
Now let’s assume your monitor was part of a perfect sphere (in other words a cap), but the pixels varied in size in a specific way:

;

Now you might be wondering what’s the significance of showing a spherical monitor when talking about planar projections. For that, let’s overlay the previous images on top of each other:

;

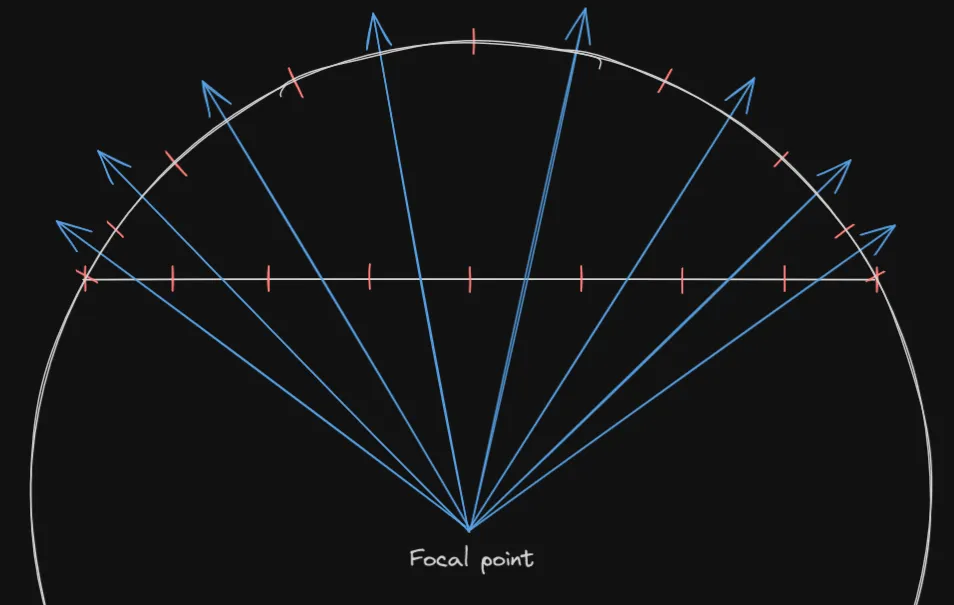
The rays in the two images are actually the same. This should tell you that the distortion you see is actually from “sampling” the image non-uniformly. If you were to visualize this, you’d get the following image:

Each ring in the previous demo is 5 degrees wide. Notice how in the center lines are relatively thino and uniform, but as you go outwards, they get thicker exponentially. This is issue only gets worse if you increase the FOV with the slider.

This means that if you were sitting directly at the “focal point” of the projection, what you’d see would be completely undistorted. But if that’s true, why can you notice it so easily in games? Simple:

Your field of view is bad

You’re probably not sitting in the focal point and if you are, you certainly won’t for long.

Here are default field of view values from a couple of noteworthy games:

• Minecraft: 70 degrees
• Team Fortress 2: 75 degrees
• Skyrim: 70 degrees
• The Witcher 3: 60 degrees
• Fortnite: 80 degrees
• Counter Strike 2: 60 degrees
• CyberPunk 2077: 75 degrees

As you can see, all of these are in the 60-80 degree range, I’ve seen games go up to 90 degrees and some people prefer to play on up to 120 degrees sometimes.

However, it’s worth asking: What’s the ideal FOV?

The ideal FOV

To answer this question, first let’s ask what FOV actually means. Most people I’ve met wrongly assumed it means the angle of the area between the left and right edges of the screen, but it’s actually the opposite, it’s the vertical angle.

To be precise, it’s usually the vertical angle, sometimes (especially in competitive or older games) it is actually the horizontal one. I didn’t check which “standard” the games in the previous list use, but they are probably close enough regardless.

Let’s do an experiment, grab some kind of measuring device, preferably one that can measure distances up to 60-70cm-s (23-27 inches). Sit down at a comfortable distance from your screen and measure it. If you’re susceptible to getting into a gamer posture, you should do that as well. For me this distance is about 57cm (the units won’t matter).

Now measure the height of your monitor (only the actual imaging part of it, leave the borders out). For me this is about 33cm.

Now it’s just simple trigonometry, we want to know the angle the monitor takes up of your vision, imagine drawing a right angle triangle between your eyes and the top and bottom of it, from this we can say that

The reason for the divisions by 2 is because I assume you’re about halfway down the monitor (hopefully this isn’t actually true, as this is bad ergonomically). The angle can actually change a bit depending on the position, but let’s disregard that.

Let’s solve for $\theta$:

Make sure to convert the result to degrees if it’s in radians. For me this resulted in 32 degrees, a far cry from the 60 degrees minimum we’ve seen in games.

Lets also try it backwards by going from a target FOV and calculating the distance you have to be from your monitor to see it perfectly:

Plugging in my own numbers and let’s say 70 for a nice middle ground I get 23cm, or about 9 inches. I’d call that too close.

So, should I lower my FOV?

You probably don’t want to, a small FOV can result in a very claustrophobic experience and it’d hinder you in competitive games. We’re surprisingly good at compensating for these distortions, so there’s not really a reason for it.

Sidequest: Projection algorithm demos

Here are a couple fun projection algorithms, I like to make articles interactive and this was a good opportunity.

Planar

Panini

Fisheye

I might add a couple more in the future if I’m bored.